오늘은 압축 센싱 기법에 대해서 알아보겠습니다. 레이더에서 중요한 건 적은 데이터로도 타깃을 정확히 찾아내는 것이 너무 중요한데요, 그것을 이루기 위한 방법 중 하나인 압축 센싱에 대해서 알아보겠습니다.
압축 센싱은 회소성과 비직교성을 이용합니다.
원래 샘플링 해야하는 데이터보다 더 적은 수의 샘플링을 함으로써 연산량을 줄이고 자원을 효율적으로 사용할 수 있다.
나이퀴스트 샘플링 이론보다 더 적은 수의 샘플링 가능
희소성이란 일반적인 신호는 전체 데이터를 다 저장해야 하지만, 우리가 원하는 정보는 보통 일부(희소한 부분)만 차지하는 경우가 많다
압축 센싱에서 데이터를 샘플링할 때, 너무 규칙적인 방식으로 샘플링하면 일부 정보만 남고 중요한 정보가 사라질 수 있다. 그래서 랜덤 하게 샘플링하는 것이 필요하다.
신호를 랜덤하게 샘플링하면 중요한 정보가 분산되어 사라지지 않는다.
압축 센싱에서는 랜덤 행렬을 측정 행렬로 사용하면 신호 복원이 잘 된다.

그림은 256개의 희소한 신호를 80개의 압축 센싱을 통해 복원한 시뮬레이션 결과물입니다. 이런 식으로 희소한 신호를 대상으로 한다면, 우리는 L1 정규화를 통해 필요한 계수만 업데이트하는 방식으로 나이퀴스트 샘플링 이론보다 적은 샘플링 수를 가지고도 중요한 정보를 복원해 낼 수 있습니다.
저는 시뮬레이션에서 LASSO 회귀를 할 수 있게 해주는 lasso 함수를 사용했습니다.
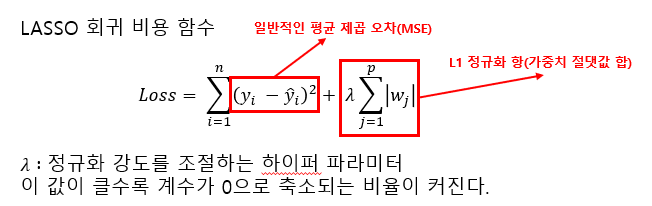
이 그림은 LASSO 회귀의 비용함수를 나타내는 식으로, 이를 최소화 하는 회귀 계산을 통해 희소 신호 복원이 이루어지게 됩니다.
하지만 요즘은 딥러닝이 나오면서 역사의 뒤안길로 사라지는 추세입니다.



댓글