오늘은 전기자기학의 기초인 벡터 해석을 위해 벡터와 스칼라에 대한 기본 개념을 알아보고 벡터를 나타내는 성분인 기본 벡터, 단위 벡터, 법 선 벡터에 대해서 알아보겠습니다. 전기자기학에서는 힘의 크기와 방향에 대한 심도 깊은 이해가 필요하기 때문에 벡터 해석에 능숙한 것은 필수입니다. 그러니 해당 내용을 기초부터 잘 쌓아나가야 합니다.
벡터와 스칼라
물리량에는 단순히 세기, 양, 정도만을 나타내는 스칼라량과 세기, 양, 정도에 더해 '방향' 정보까지 포함하는 벡터량이 있습니다.
스칼라(scalar)
앞서 언급한 것처럼 크기정보만 가지고 있는 물리량입니다. 길이, 온도, 전위, 에너지, 일 등의 물리량을 나타내는 데 쓰입니다.
벡터(vector)
반대로 벡터는 '크기와 방향을 가지고 있는 물리량'입니다. 힘, 속도, 가속도, 회적력(토크) 등 크기에 더해 방향 정보까지 포함하는 물리량을 나타내는 데 쓰입니다.
벡터의 표기
보통 벡터를 표기할 때는 다음과 같이 표기합니다. 시험에서 어떤 형태로 나타낼 질 모르기 때문에 모두 알아두셔야 할 것입니다.

가장 좌측처럼 획을 하나 더하거나, 문자 위에 점이나 화살표를 적어 나타내기도 하고, 문자를 다른 문자보다 진하게 표기해 스칼라 값과 구분하기도 합니다.
이것들에 더해, 벡터는 크기(스칼라량) x (기본벡터/단위벡터/법선벡터)로 나타낼 수 있습니다.
크기에 곱해지는 벡터들은 방향 정보를 담고 있습니다. 크기에 영향을 주면 안 되므로 이 방향벡터들은 크기가 모두 1이라고 볼 수 있습니다. (당연하지만 어떤 수에 1을 곱하면 변화가 없습니다.)
- 크기 x (기본벡터/단위벡터/법선벡터) ➡️ 방향 정보만 나타내야 하므로 이 벡터들은 크기가 무조건 1(방향벡터)
다음으로는 방향벡터들을 하나씩 알아보겠습니다.
기본벡터(base vector)
기본 벡터에서도 원통형 좌표계, 구면 좌표계 등이 있지만 오늘은 직각 좌표계(직교 좌표계)에서의 기본 벡터에 대해서 알아보겠습니다.
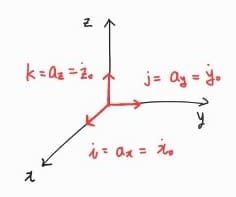
사진에서와 같이 직각좌표계는 3차원 좌표계로, 각 축들이 직각이라는 특징이 있습니다.
- 원점에서 x축으로 향하고 크기가 1인 벡터를 i, (벡터 이름) x, x₀ 등으로 나타냅니다.
- 원점에서 y축으로 향하고 크기가 1인 벡터를 j, (벡터이름)y, y₀ 등으로 나타내고
- 원점에서 z축으로 향하고 크기가 1인 벡터를 k, (벡터 이름) z, z₀ 로 나타냅니다.
직각 좌표계에서 임의의 벡터 A가 다음과 같다고 정의해봅시다. 스칼라 x 기본벡터의 형태로 벡터를 나타내면 벡터 A는 다음과 같이 나타낼 수 있습니다.
A = ai + bj + ck(a, b, c는 상수)
그렇다면 벡터 A의 크기는 어떻게 구하면될까요?
A의 크기는 A의 절댓값입니다. A의 절댓값을 구하기 위해서 각 성분의 크기들의 피타고라스 합을 구해주시면 되겠습니다.(방향 성분이 다르기 때문에 절대 그냥 더해서는 안됩니다.) A 벡터의 크기를 구하는 식은 다음과 같습니다.

- 벡터 절댓값 = 벡터 크기, 성분이 다르기 때문에 그냥 더할 수 없다. ➡️ 피타고라스 정리 이용 절댓값 크기 구하기.
단위 벡터(unit vector)
단위 벡터는 기본 벡터를 포함하는 벡터로, 크기가 1인 모든 벡터를 단위 벡터라고 합니다. 방향 정보가 어떻든 크기를 1로 만들기만 하면 단위 벡터를 계산할 수 있습니다. 마찬가지로 A = ai + bj + ck(a, b, c는 상수)라고 할 때 계산 방법은 다음과 같습니다.

이렇게 만들면 크기가 1인 단위 벡터가 완성이 됩니다. 이렇게 만들어진 단위 벡터(unit vector)는 보통 앞글자를 따 u, û 등으로 쓰입니다.
법 선 벡터(수직 벡터, normal vector)

법 선 벡터는 수직벡터라고도 부릅니다. 크기가 1이면서 사진과 같이 폐곡면에 대해 수직인 벡터를 바로 법선벡터라고 합니다. 법선벡터는 normal vector 이므로 앞글자를 따 약자 n, ṅ으로 쓰입니다. 이 법선벡터는 보통 회전 벡터의 진행방향을 표시할 때 사용합니다. 전자기학에서는 전기력선의 진행방향을 나타낼 때 쓰입니다.

댓글